

Using Fibonacci heaps for priority queues improves the asymptotic running time of important algorithms, such as Dijkstra's algorithm for computing the shortest path between two nodes in a graph, compared to the same algorithm using other slower priority queue data structures. It is also possible to merge two Fibonacci heaps in constant amortized time, improving on the logarithmic merge time of a binomial heap, and improving on binary heaps which cannot handle merges efficiently. A Fibonacci heap is thus better than a binary or binomial heap when b is smaller than a by a non-constant factor. In a binary or binomial heap such a sequence of operations would take O((a + b) log n) time. This means that starting from an empty data structure, any sequence of a insert and decrease key operations and b delete operations would take O(a + b log n) worst case time, where n is the maximum heap size. Deleting an element (most often used in the special case of deleting the minimum element) works in O(log n) amortized time, where n is the size of the heap. The insert and decrease key operations also work in constant amortized time. For example, merging heaps is done simply by concatenating the two lists of trees, and operation decrease key sometimes cuts a node from its parent and forms a new tree.įor the Fibonacci heap, the find-minimum operation takes constant (O(1)) amortized time. This flexibility allows some operations to be executed in a "lazy" manner, postponing the work for later operations. The trees do not have a prescribed shape and in the extreme case the heap can have every element in a separate tree. This implies that the minimum key is always at the root of one of the trees. Let's look at what needs to be done in each function of Stack using the functions addFirst, removeFirst and getFirst.A data structure that is a collection of trees satisfying the minimum-heap property, that is, the key of a child is always greater than or equal to the key of the parent. Whereas the function removeLast which we implemented takes O(n) time, therefore we discard the idea of operating at the end of the linked list. take constant time to perform their action. We do so because the functions addFirst, getFirst and removeFirst are of O(1) i.e. take constant time to perform their action.īut if you use the linked list which we implemented then we chose to operate the starting of the linked list. If we use the linkedlist which is in java then it does not matter which way we choose to do it because addition and removal at end as well as beginning are O(1) i.e. We have two options to achieve this: we can perform these operations like addition and removal either at the beginning or at the end.

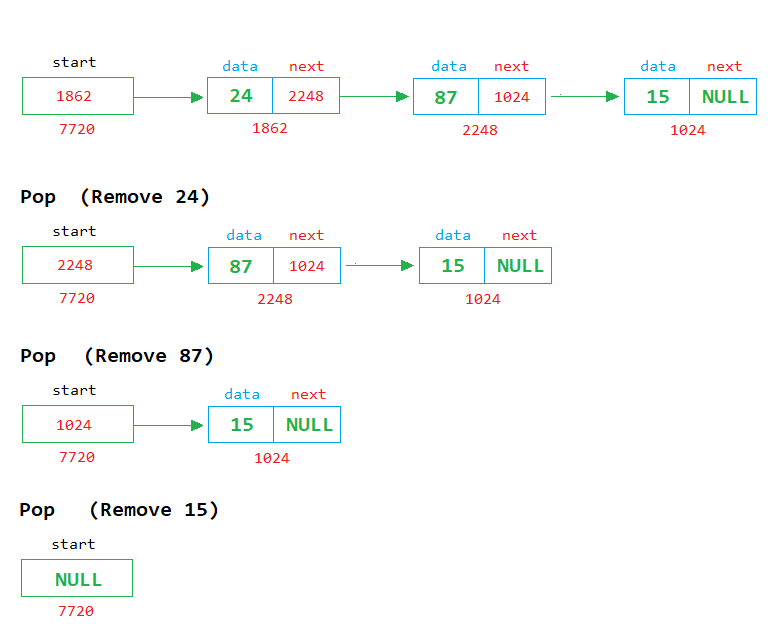
To make a linked list work like a stack, we need to make use of functions, such that addition and removal occurs at one end only. Element is removed and added from one end only. Which means, the end at which element will be added lastly will be the first to get accessed. As we know, it is also given in the question that Stack adds and removes elements in LIFO manner, i.e. We will look at each function of our Stack Adapter individually. Reverse Linked List (pointer - Recursive) Remove Duplicates In A Sorted Linked Listĭisplay Reverse (recursive) - Linked List


 0 kommentar(er)
0 kommentar(er)
